【数学の学習に主体的に取り組む子どもを育成する指導⑥】多様な解法のある問題を扱ってください

はじめに

数学の学習に主体的に取り組む子どもを育成するために、教育現場として取り組むべき課題とは何か。現在、東京都教職員研究センターで東京教師道場の担当をし、指導力向上のためにがんばっている先生方の指導を行っている小宮賢治先生に、この大きな課題を解決するための、指導上の要点や、子どもたちとの向き合い方について、記事をご執筆いただきました。

今回は第6回として、【数学の学習に主体的に取り組む子どもを育成する指導】をテーマにご執筆いただいた「多様な解法のある問題を扱ってください」を紹介します。

本記事の執筆にあたっての小宮先生からのメッセージはこちらの記事をご覧ください。
SAMEにおける「数学の学習に主体的に取り組む子どもを育成する指導」の執筆にあたって

多様な解法のある問題を扱ってください

問題解決の授業では、多様な解法のある問題をできるだけ設定できるように努力してほしいと考えます。多様な解法があることで、すべての子どもが取り組みやすくなるという利点があります。また、学級全体でいろいろな考えを共有するなかで多様な解法に学び、学びを深めることができます。さらに、発表された考えを練り上げるなかで、問題解決における解法の基本的な考え方を見いだしたり、新たな解法を見つけたりすることが期待されます。

たとえばですが、中学校第２学年の領域「図形」の「基本的な平面図形の性質」を学習するなかで、下の図のようなブーメランの形をした凹四角形の∠xを求めるような問題が考えられます。

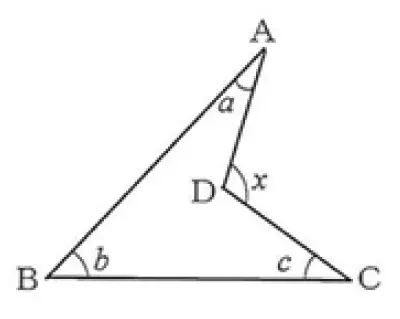
解法の１つには、点Ｄを通ってＢＣに平行な直線を引いて「平行線の同位角、錯角は等しい」ことと「三角形の外角は、それととなり合わない２つの内角の和に等しい」ことを用いて解決する場合があります。

解法の２つには、ＡＤを延長して凹四角形を２つの三角形に分けて、「三角形の外角は、それととなり合わない２つの内角の和に等しい」ことをくり返し用いて解決する場合があります。

解法の３つには、点ＢとＤを結んで点Ｄの方向に延長して、△ＢＤＡと△ＢＣＤのそれぞれで「三角形の外角は、それととなり合わない２つの内角の和に等しい」を用いて解決する場合があります。

解法の４つには、点ＡとＣを結び、△ＡＢＣと△ＡＤＣのそれぞれで「三角形の内角の和は１８０°である」ことを用いて解決する場合があります。

以上の４つの解法が生徒から出てきたとします。全体で共有するなかで、自身の解法とは異なる解法について、生徒は発表から学ぶことになります。

そのなかで、「平行線の性質」や「三角形の内角、外角の性質」の利用のしかたについても学ぶことになります。また、そうした性質を利用するには、補助線を引くことの大切さも学ぶことになります。学びが深まっていくことになります。

さらに、全員で考察し練り上げるなかで、∠xを求めるには、あらかじめ示されてわかっている角度に着目することが大切だということに気づくものと考えられます。そうすると、子どものなかから、ＢＣに平行な直線は、点Ｄだけでなく点Ａを通る直線も考えると、平行線の性質だけで説明することができるといった考えや、点Ｄを通りＢＣとＡＢに平行な直線を考えると、平行線の性質だけで説明することができるといった考えも出てくることが考えられます。子どもたちの学びがますます深まることになります。

多様な解法のある問題を扱うことで、こうした学びを子どもは得ることができると考えます。多様な解法のある問題を授業で取り上げることを心がけていただければ幸いです。

本稿の執筆者 小宮賢治

公益財団法人 日本数学検定協会 理事

東京都公立中学校長、東京都中学校数学教育研究会会長等を歴任。現在は、東京都教職員研修センター 学習指導員（東京教師道場）として、数学の指導力を高めようとがんばっている先生方の指導を行っています。