
電気と数学(その4)-半導体の整流特性:物性物理学と数学との交点-
- 数学
- 半導体
- 電子
- 正孔
- pn接合
- 物性物理学

「ライフサイエンス」とは, 数学や物理学の理論を駆使して生命現象や生態系の研究を行う分野で「数理生命科学」とも深い関わりをもっています。「ライフサイエンス」は関心ある現象に対して,生命現象の諸関係を数式やアルゴリズムで表現した「数理モデル」をつくり,このモデルの解析を通じて,生命現象や生物の振る舞いに対する理解を数理的観点から深めることを目的としています。
本記事では,生命現象のなかでもとくに人口や生物個体数の増加というひじょうに身近な事象に絞って,微分方程式の数学的手法を用いた数理モデルと,数理モデルによって分析した結果を紹介します。
 図1
図1
イギリスの経済学者マルサスは,『人口論』の1798年の初版(図1)で,人口は人間の本能である性欲により幾何級数的に増加するのに対して,食料は算術級数的にしか増加しないと唱えました。
つまり,人口を制限しなければ,食料資源は必ず不足し貧困が始まるという帰結を説いたのです。
図2では,人口 は時刻 に対し幾何級数的増加の例として\(N=2^t\) ,また食料\(N\) は時刻\(t\) に対し算術級数的増加の例として\(N=50t\) のグラフをそれぞれ示します。
時間の推移とともに人口と食料も増加しますが,\(t=7\) あたりから人口は急激な増加に転じ,赤★のところで人口は食料を超過して,マルサスの指摘する食料資源の不足が始まることになります。
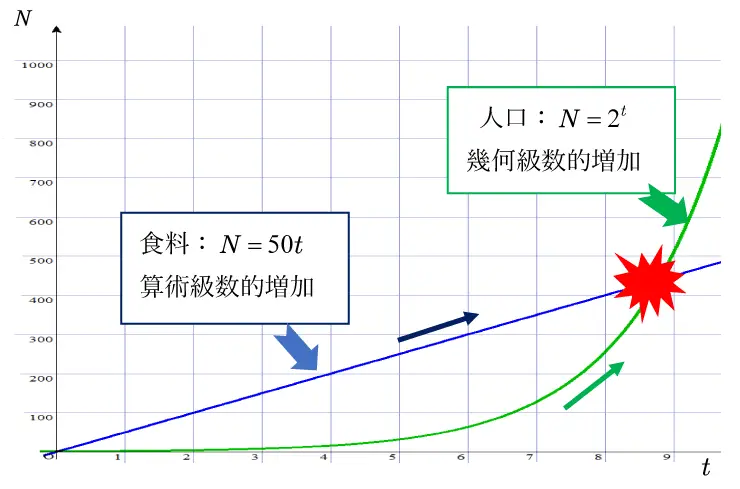 図2
図2算術級数的増加と幾何級数的増加を数学的に考えてみましょう。人口(生物個体数)を\(N\) , 時間を\(t\) とすれば,算術級数的増加は,\(N=at\) (定数\(a>0\) )で表されます。この場合,\(N\)を\(t\)で微分しますと,微分方程式
\(\displaystyle \frac{dN}{dt}=a\) (定数\(a>0\) ) …①
が得られます。
すなわち,\(N\)が増加する割合(導関数)は一定値\(a\) となり,\(N\)は時間の推移とともに一定の割合で増加していきます。\(t=0\)のとき,\(N=0\)であれば,これは原点を通る直線になります。
一方,幾何級数的増加は,\(N=a^t\) (定数\(a>1\) )と表されますので,
両辺の自然対数をとって,\(\log_{e}N=t\log_{e}a\) (定数\(a>0\) )
上式の両辺を\(t\) で微分すると,\(\displaystyle \frac{1}{N} \displaystyle \frac{dN}{dt}=\log_{e}a\) , \(\displaystyle \frac{dN}{dt}=N\log_{e}a\)
よって,微分方程式
\(\displaystyle \frac{dN}{dt}=AN\) (定数\(A=\log_{e}a\) ) …②
が得られます。
なお、\(a=e\)の場合は,\(N=e^t\) (\(e\) :自然対数の底)となって,\(A=\log_{e}e=1\) より
微分方程式②はシンプルに\(\displaystyle \frac{dN}{dt}=N\) と表すことができます。
算術級数的増加を表す①は直線で,\(N\)が大きくなっても\(N\)が増加する割合(導関数)は一定で変わりません。
一方,幾何級数的増加の②は,\(N\)が増加する割合(導関数)は\(N\)に比例しており,\(N\)が大きくなればなるほど,指数関数的に大きく増加していくことがわかります。
この結果,図2において,幾何級数的増加の曲線は,算術級数的増加の直線を赤★の箇所から超過することに納得がいくでしょう。
1838年にベルギーの数学者ピエール=フランソワ・フェルフルスト(Pierre-François Verhulst)によって,ロジスティック方程式は発案されました。フェルフルストは,前章で出てきたマルサスの『人口論』における人口は指数関数的に増加するという点に対し,現実的には環境や資源は限られているため,人口増加にはいずれブレーキがかかって,ある一定値に落ち着くと考えたのです。ロジスティック方程式はこの点を取り入れて,生物の個体数増加の抑制(ブレーキ)をモデル化したものです。
ロジスティック方程式は具体的には,
\(\displaystyle \frac{dN}{dt}=rN\begin{pmatrix} 1- \displaystyle \frac{N}{K}\end{pmatrix} \) …③
という微分方程式で表されます。
ここで\(N\) は個体数,\(t\) は時間,\(r\)は内的自然増加率とよばれ, \(r\)が大きいほど個体数増加率\(\displaystyle \frac{dN}{dt}\)が大きくなり,個体数\(N\)が増加していきます。
また,\(K\)は環境収容力と呼ばれる定数で,爆発的に増加する個体数\(N\)にブレーキをかける効果をもちます。すなわち,個体数\(N\)が増えて環境収容力\(K\) に近づくほど,\(N/K\)は1の値に近づくので③の右辺も0に近づき,結果的に個体数増加率\(\displaystyle \frac{dN}{dt}\)が減って,\(N\)が環境収容力に近づいていく(すなわち収束する)モデルになります。
③の解は,時間\(t=0\)で初期個体数を\(N_{0}\) とすると,\(N=\displaystyle \frac{K}{1+(K/N_{0}-1)e^{-rt}}\) となります。
なお,微分方程式③の解法は<参考2>を参照してください。
さて,\(N=\displaystyle \frac{K}{1+(K/N_{0}-1)e^{-rt}}\) において,\(t\to\infty\)で,\(e^{-rt}\to0\) より,\(N\to K\) (環境収容力)と,人口\(N\)は環境収容力\(K\) に収束します。これからマルサスが指摘したような人口が(食料を超えて)無限大にならないことが分かります。
また,\(K/N_{0}=1\),すなわち\(K=N_{0}\) のときは,\(N=N_{0}(=K)\) の一定値のままです。
ここで,\(N=\displaystyle \frac{K}{1+(K/N_{0}-1)e^{-rt}}\) において,仮に定数 \(K=100\),\(r=1\)の値に設定し,初期個体数 \(N_{0}=0.1K\) , \(0.25K\) , \(0.5K\) , \(0.75K\), \(K\), \(2K\), \(10K\)の値に変化させて,グラフを描いてみると,図3のようになります。
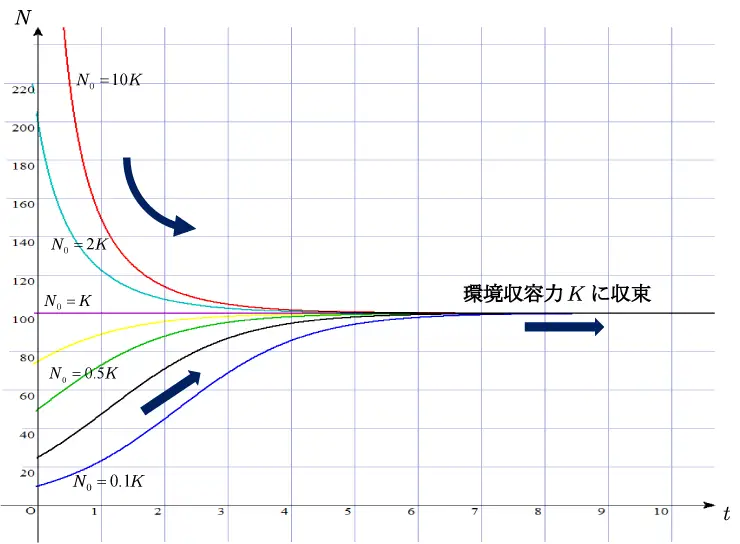 図3
図3
すなわち, すべてのグラフは最終的には傾きは0になり,環境収容力\(K\)に収束する水平な直線となることが分かります。
\(\displaystyle \frac{dN}{dt}=\displaystyle \frac{r}{K}N(K-N)\)より,\(0<N<K\)では\(\displaystyle \frac{dN}{dt}>0\)で
\(N\)は時間\(t\)とともに増加するが, \(K-N\)は0に近づいて, \(N\)の増加が鈍化します。
一方, \(K<N\)では,\(\displaystyle \frac{dN}{dt}<0\)より, 時間\(t\)とともに減少するが, この場合も\(K-N\) は0に近づいて,\(N\)の減少が鈍化します。
この性質を示したものが図4のグラフになります。
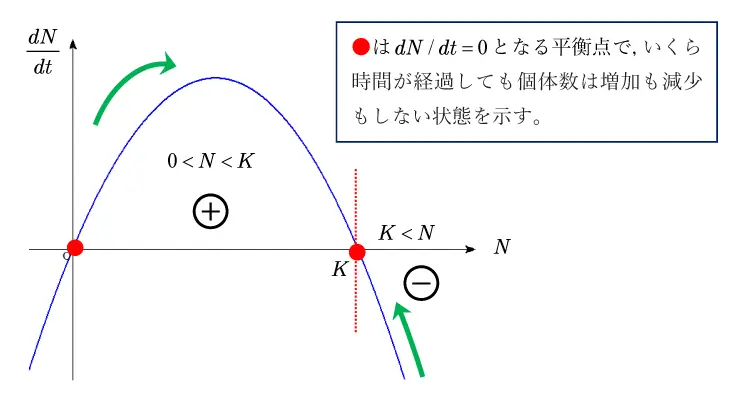 図4
図4
これらはともに,\(N\)が最終的には環境収容力の一定値\(K\)に収束することを示しています。
なお,幾何級数的増加の場合,\(\displaystyle \frac{dN}{dt}=AN\)と表され,個体数(人口)\(N\)が大きくなるほど\(N\)の増加率がどんどん増加して,\(N\)の値は歯止めが効かないモデルですが,上記からもロジスティック方程式③では\(N\)の値はブレーキが効いて一定値になる構造になっています。
\(\displaystyle \frac{dN}{dt}=rN\begin{pmatrix} 1- \displaystyle \frac{N}{K}\end{pmatrix} \)は変数分離形として,以下のように解くことができます。
\(\displaystyle \frac{dN}{dt}=\displaystyle \frac{r}{K}N(K-N)\)を変形して,\(\displaystyle\int\frac{dN}{N(K-N)}=\displaystyle \frac{r}{K}\int{dt}\)
\(\displaystyle\frac{1}{K}\int\begin{pmatrix}\displaystyle \frac{1}{N}+\displaystyle \frac{1}{K-N}\end{pmatrix}dN=\displaystyle\frac{r}{K}t+c\)
\(\displaystyle\frac{1}{K}\log_{e} \displaystyle\frac{N}{|K-N|}=\displaystyle\frac{r}{K}t+c\),\(\log_{e}\displaystyle\frac{N}{|K-N|}=rt+C\)
\(\displaystyle\frac{N}{|K-N|}=C'e^{rt}\),\(\displaystyle\frac{N}{K-N}=\pm{C'e^{rt}}=A^{rt}\) (上式での\(c\),\(C\),\(C'\),\(A\)はすべて定数)
\(\displaystyle\frac{N}{K-N}=Ae^{rt}\)…④ より,\(KAe^{rt}-NAe^{rt}=N\) ,よって\(N=\displaystyle\frac{KAe^{rt}}{1+Ae^{rt}}\) …⑤
初期条件\(t=0\) のとき,\(N=N_{0}\)とすれば,④より\(A=\displaystyle\frac{N_{0}}{K-N_{0}}\) でこれを⑤に代入すれば,
| \(N=\displaystyle\frac {\displaystyle\frac{KN_{0}}{K-N_{0}}e^{rt}}{1+\displaystyle\frac{N_{0}}{K-N_{0}}e^{rt}}=\displaystyle\frac{KN_{0}}{(K-N_{0})e^{-rt}+N_{0}}=\displaystyle\frac{K}{(K/N_{0}-1)e^{-rt}+1}\) |
が最終的に得られます。
\(t<0\),\(N<0\)を含めたグラフの全容を図5で示します。
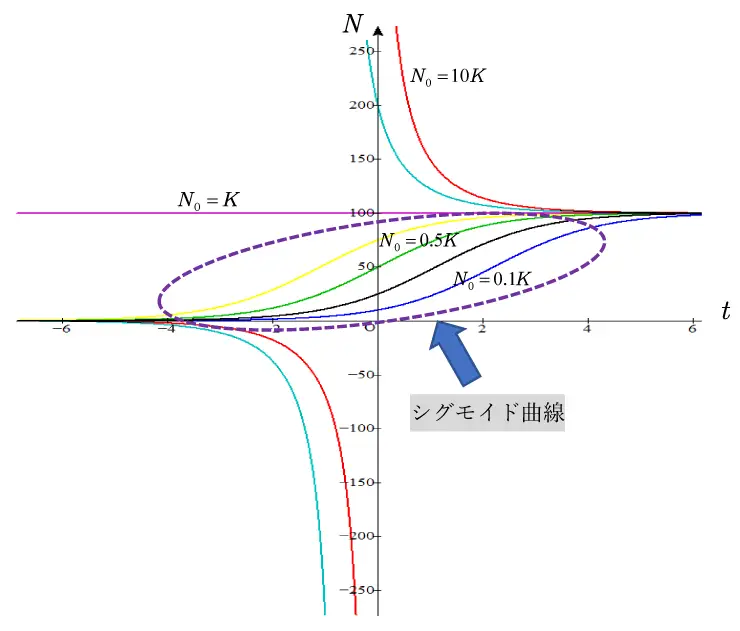 図5
図5
とくに\(K/N_{0}>1\)(\(i.e. 0<N_{0}<K\))の範囲(破線部分)では,グラフは変曲点をもつアルファベットのS字型になり,シグモイド曲線とも呼ばれます。シグモイド曲線は一般的には,\(y=\displaystyle\frac{1}{1+e^{-ax}}\) (\(a>0\))で表され,\(t\to-\infty\) のとき\(y\to0\) ,\(t\to\infty\) のとき\(y\to1\) の単調増加関数で,\(x=0\)で1つの変曲点をもつS字型の形状をもちます。
\(N=\displaystyle\frac{K}{1+(K/N_{0}-1)e^{-rt}} \) においても,\(K/N_{0}>1\)より,\(t\to\infty\)のとき\(N\to K\),\(t\to-\infty\)のとき\(N\to0\)となって,図5で示すようにS字型の形状となります。
前章までは,1つの個体すなわち単数の生物個体数の増加について論じてきました。本章では,2種類の生物個体が影響し合って個体数がどのように変化するかについて触れることにします。
イタリアの生態学者ダンコナは,漁業操業が低下した第一次世界大戦中に食用魚よりもサメの年間漁獲率が増加したことに疑問をもち,ヴォルテラに打診したところヴォルテラがこの現象を説明するためにロトカ・ヴォルテラの方程式を発案したと言われています。
ロトカ・ヴォルテラの方程式は,2生物間の捕食-被食関係による個体数の変動を表現する数理モデルの一種で,被食者\(x\)(食われるもの)と捕食者\(y\) (食うもの)との相互作用を記述する以下のような微分方程式⑥,⑦で表されます。
数学的には1階の連立常微分方程式で,生態学者ダンコナの実例では被食者\(x\)が食用魚に,また捕食者\(y\)がサメに相当します。
| \(\begin{equation}\left \{\begin{array}{l}\displaystyle\frac {dx}{dt}=\alpha{x}-\beta{xy} (\alpha>0, \beta>0 ) …⑥\\\displaystyle\frac {dy}{dt}=-\gamma{y}+\delta{xy} (\gamma>0, \delta>0 ) …⑦ \end{array}\right.\end{equation} \) |
ここで,\(\alpha\) ,\(\beta\) , \(\gamma\) , \(\delta\) は正の定数で,\(\alpha\) ,\(\gamma\) はそれぞれ被食者,捕食者の内的自然増加率を,また\(\beta\) は被食者が捕食者に捕食される割合を,\(\delta\) は捕食者が被食者を捕食する割合をそれぞれ表します(図6)。
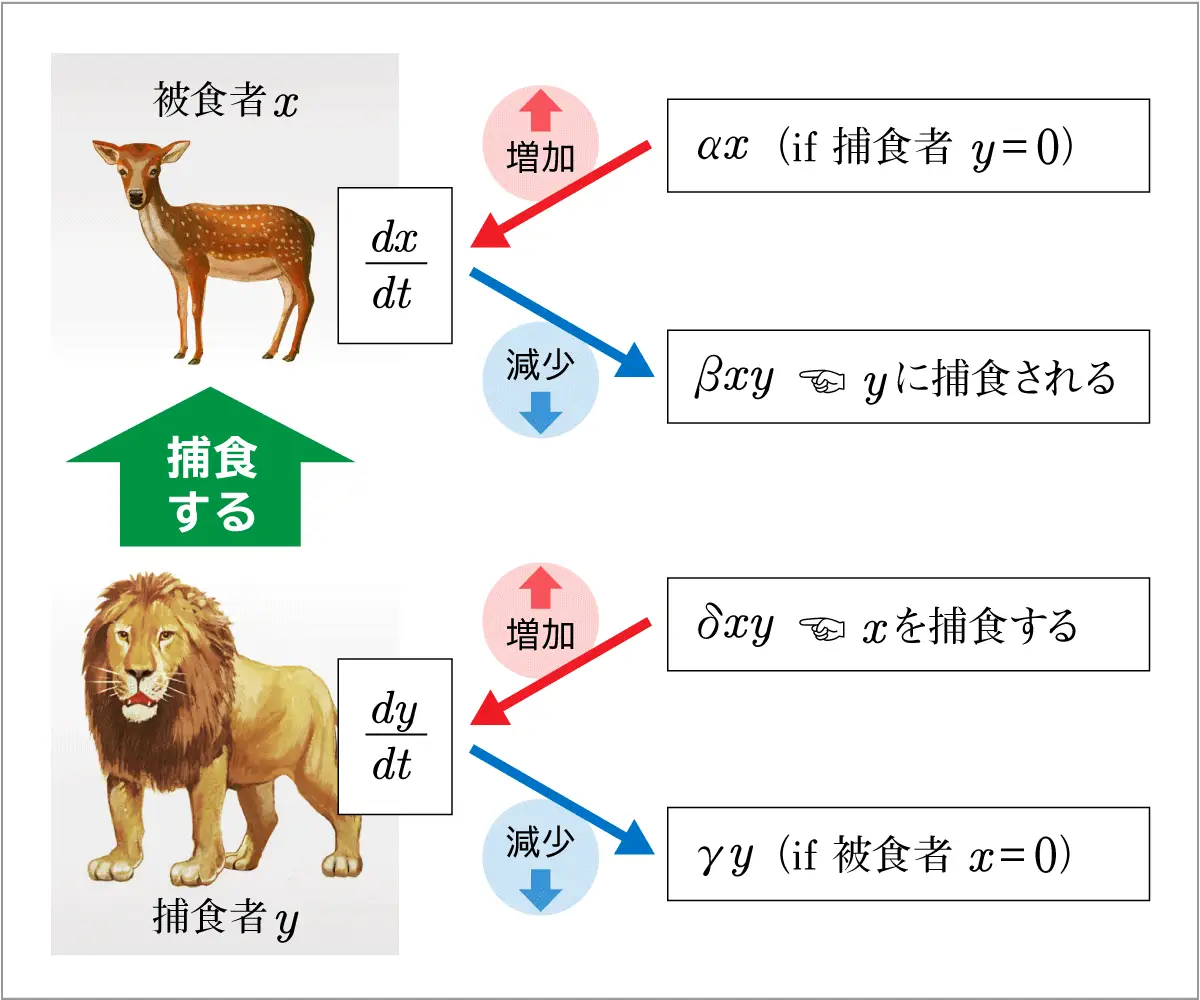 図6
図6
定数\(\alpha=1\) ,\(\beta=0.03\) , \(\gamma=1\) , \(\delta=0.025\) に対して,上式⑥,⑦をプログラミング言語Pythonを用いてシミュレーションした結果を図7に示します。
図7より被食者と捕食者の個体数がともに位相がずれた周期的な動きをしていることが見てとれます。すなわち,被食者が増加すれば捕食者も後を追うように増加し,被食者が減少に転ずれば捕食者も後を追うように減少していく様子が再現できています。
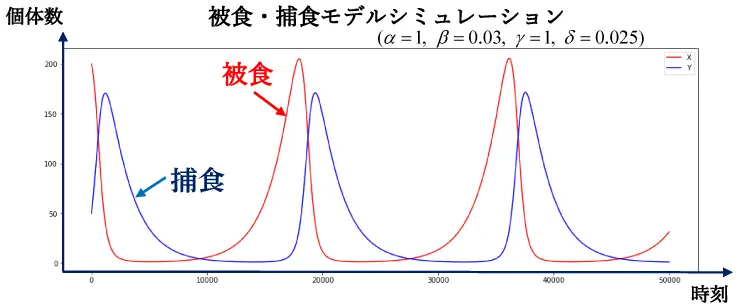 図7
図7また被食者と捕食者の周期的な増減を違う角度から分析してみます。
⑥と⑦より,次の微分方程式が得らます。
\(\displaystyle\frac{dy}{dx}=\displaystyle\frac{dy/dt}{dx/dt}=\displaystyle\frac{(-\gamma+\delta{x})y}{(\alpha-\beta{y})x}\) …⑧
⑧は変数分離形なので,以下のように解くことができます。
\(\displaystyle \int\displaystyle\frac{\alpha-\beta{y}}{y}dy=\displaystyle \int\displaystyle\frac{-\gamma+\delta{x}}{x}dx\)
\(\alpha\log_{e}y-\beta{y}=-\gamma\log_{e}x+\delta{x}+C\) (\(C\):定数)
\(\log_{e}y^{\alpha}x^{\gamma}=\beta{y}+\delta{x}+C\)
\(y^{\alpha}x^{\gamma}=Ae^{\beta{y}+\delta{x}}\) (定数\(A=e^{C}\))より,
\(\displaystyle\frac{y^{\alpha}x^{\gamma}}{e^{\beta{y}+\delta{x}}}=A\) …⑨
が得られます。
⑨の\(\alpha,\beta,\gamma,\delta\)に適当な値(\(\alpha=1\),\(\beta=0.03\),\(\gamma=1\), \(\delta=0.025\))を設定すると,図8のような解\(x,y\)の軌跡が描けます。
なお,⑧において,\(x=y=0\) また\(\displaystyle\frac{\gamma}{\delta}\) ,\(y=\displaystyle\frac{\alpha}{\beta}\)では,\(x=\displaystyle\frac {dy}{dx}=0/0\)となります。
この2点\((0,0)\),\(\begin{pmatrix}\displaystyle\frac {\gamma}{\delta},\displaystyle\frac {\alpha}{\beta} \end{pmatrix}\)を平衡点とよび,図8で●で示します。
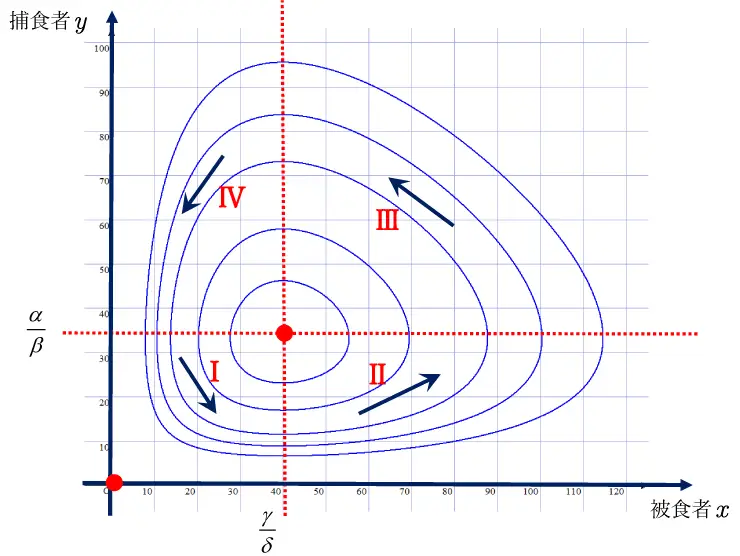 図8
図8
図8より解\(x,y\)の軌跡は閉じているので,周期的であることがわかります。
図8で示した領域IからⅣまでの特徴を説明します。
\(\displaystyle\frac {dx}{dt}=(\alpha-\beta{y})x>0\),\(\displaystyle\frac {dy}{dt}=(-\gamma+\delta{x})y<0\)
被食者\(x\)不足のため捕食者\(y\)も減少するが,
捕食者\(y\)が減少するため,被食者\(x\)は増加する。
\(\displaystyle\frac {dx}{dt}=(\alpha-\beta{y})x>0\),\(\displaystyle\frac {dy}{dt}=(-\gamma+\delta{x})y>0\)
被食者\(x\)が増加するため,捕食者\(y\)も増加する。
\(\displaystyle\frac {dx}{dt}=(\alpha-\beta{y})x<0\),\(\displaystyle\frac {dy}{dt}=(-\gamma+\delta{x})y>0\)
捕食者\(y\)が増加するため, 被食者\(x\)は減少する。
\(\displaystyle\frac {dx}{dt}=(\alpha-\beta{y})x<0\),\(\displaystyle\frac {dy}{dt}=(-\gamma+\delta{x})y<0\)
被食者\(x\)が減少するため,捕食者\(y\)も減少する。
ロトカ・ヴォルテラの方程式で示された被食者と捕食者の個体数の周期的な挙動で野外環境における実例としては,カナダにおいてカンジキウサギとその捕食者であるカナダオオヤマネコの個体数が長期間にわたって振動(周期的な挙動)していた実測データが挙げられます。
本記事では,「ライフサイエンス」における生命現象のなかでもとくに人口と生物個体数の増加という身近な生物学的事象に絞った「数理モデル」を紹介しました。
数学的手法として,常微分方程式によるモデルを主にしておりますが,数学的技法にも関心をもっていただけるように微分方程式の解法(変数分離形)にはていねいな導出を加えました。
本記事を通じて,ライフサイエンスの数理モデルに興味・関心をもってくださる方が1人でも多く現れることを願っています。
なお,本記事の続編として,最近話題になっている「感染症流行」のモデル化について触れた記事を公開する予定です。「感染症流行」のモデル化といっても本記事で紹介した数学的アプローチと異なるのではなく,同じ微分方程式による数理モデルを用いて現象を分析することができます。

学習数学研究所 研究員