
電気と数学(その4)-半導体の整流特性:物性物理学と数学との交点-
- 数学
- 半導体
- 電子
- 正孔
- pn接合
- 物性物理学

ライフサイエンス数学(その1)の記事では,生命現象のなかでもとくに人口や生物個体数の増加という身近な生物学的事象に絞って,微分方程式という数学的手法を用いた数理モデルとその分析結果を紹介しました。
本記事では,その1における数理モデルの延長として局地的・閉鎖的な集団に感染性の病気が持ちこまれたとき,その集団のなかでどのくらいの人口が感染していくかという問題に関して,ケルマック&マッケンドリックのSIRモデルの構造や基本的特徴から考察してみます。
SIRモデルは,1927 年にイギリスのケルマックとマッケンドリック(Kermack&McKendric)による微分方程式のことで,人口集団における感染症流行を記述する数理モデルとして,当時の感染状況をよく再現できることを示しました。SIRモデルにおいては,以下3種類の人口区分を考えます。
・\(S(t)\) :未感染者(susceptibles:感染する可能性のある人数)
・\(I(t)\) :感染者(infectives:感染し,かつ感染させる能力のある人数)
・\(R(t)\) :免疫保持者・死者(recoverd: 病気から快復した免疫保持者,ただし死亡者含む)
上記それぞれに対して,ケルマックとマッケンドリックは以下の連立常微分方程式(①,②, ③)によって表されるSIRモデルを提唱しました。
\begin{cases}
\displaystyle\frac{dS(t)} {dt} =-\beta S(t)I(t) …①\\
\displaystyle\frac{dI(t)} {dt} =\beta S(t)I(t)-\gamma I(t) …②\\
\displaystyle\frac{dR(t)} {dt} =\gamma I(t) …③
\end{cases}
\(\beta\):感染率,\(\gamma\):除去率(感染者ではなくなる(快復or死亡)率)
微分方程式①, ②, ③を図式化すると図1のようになります。
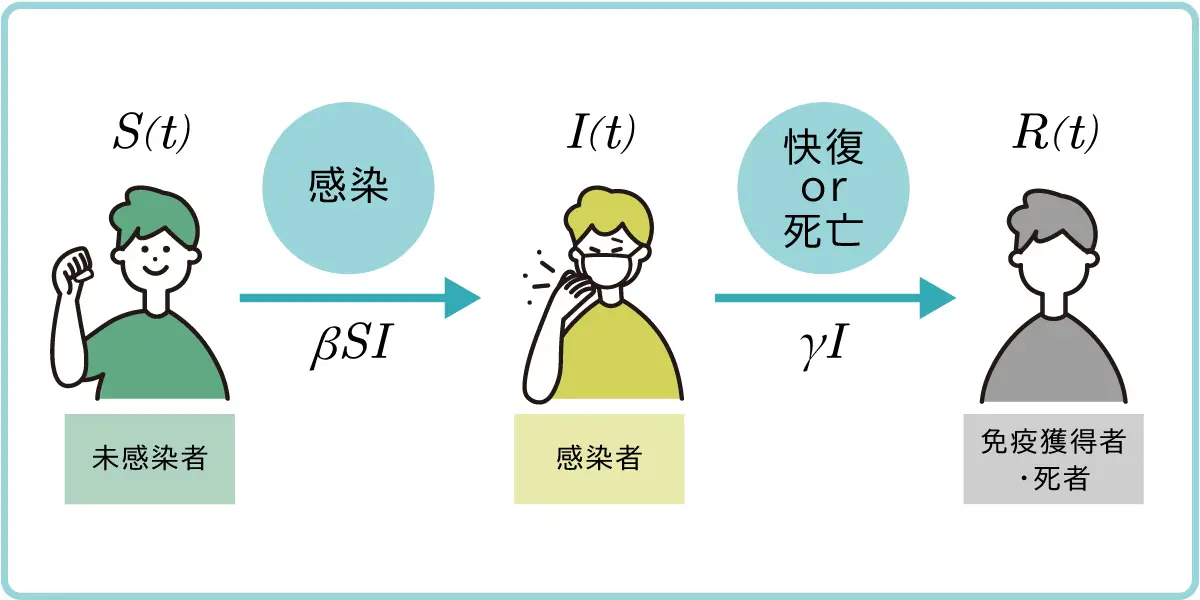 図1
図1
上記3つの微分方程式 ①, ②, ③は,
①は,未感染者\(S(t)\)は,感染者\(I(t)\)の係数\(\beta\)倍に比例して減少する傾向
②は,感染者\(I(t)\)は,感染可能人数\(S(t)\)の係数\(\beta\)倍に比例して増加する一方,感染者\(I(t)\)の係数\(\gamma\) 倍に比例して減少する傾向
③は,病気から快復した人数\(R(t)\)は,感染者\(I(t)\)の\(\gamma\)倍に比例して増加する傾向
をそれぞれ表します。
ここで,とくに微分方程式②について考えてみます。
②において,流行初期の感受性人口を\(S(0)\)とすると,
\(\displaystyle\frac{dI(t)}{dt}=(\beta S(0)-\gamma)I(t)\) …④
を解くと,
\begin{align}
I(t)&=I(0)e^{(\beta S(0)-\gamma)t}\\
&=I(0)e^{\gamma(R_0-1)t}
\end{align}
となります。
基本再生産数(Basic reproduction number) \(R_0=\displaystyle\frac{\beta S(0)}{\gamma} \begin{cases}>1\\=1\\<1\\\end{cases}\)
に応じた\(I(t)\)の時間的推移を図2に示します。
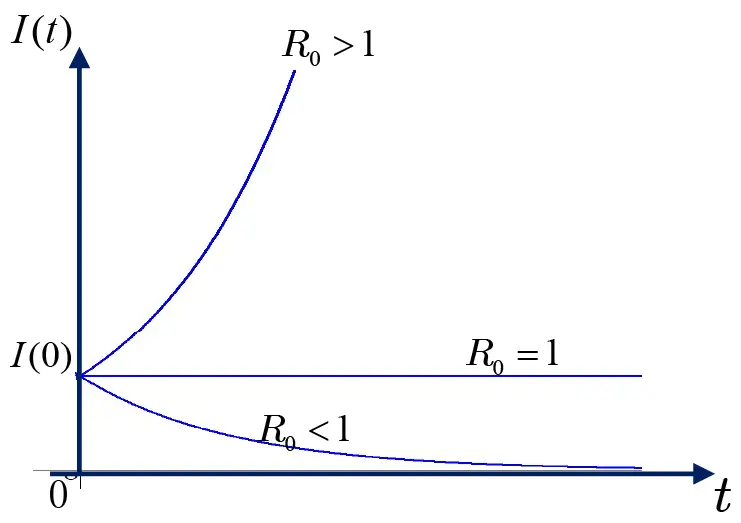 図2
図2
すなわち,基本再生産数\(R_0\)が
\begin{equation}\left \{\begin{array}{l}\text{・1超であれば,感染者数}I(t)\text{は増加傾向}\\\text{・1に等しければ,感染者数}I(t)\text{は初期値}I(0)\text{を保持(一定)}\\\text{・1未満であれば,感染者数}I(t) \text{は減少傾向}\end{array}\right.\end{equation} |
であることをそれぞれ表します。
微分方程式④の解法を以下に示します。
④は変数分離形なので,
\begin{align}
\displaystyle\int\frac{dI}{I}dt&=\int(\beta S(0)-\gamma)dt\\
\log_{e}I (t)&=(\beta S(0)-\gamma)t+c \text{(}c\text{:定数)}\\
I(t)&=Ae^{(\beta S(0)-γ)t} \text{ (}A=e^c\text{:定数)}
\end{align}\(t=0\)のとき,\(I(0)=A\)より,\(I(t)=I(0)e^{(\beta S(0)-\gamma)t} \) が得られます。
指数\((\beta S(0)-\gamma)\)の値が正, 0,負により,感染者数\(I(t)\)がそれぞれ指数的増加,初期値\(I(0)\)のままの一定値,減少して0に収束していくとなります。
すなわち,
\begin{align}
\beta S(0)-γ>0 ⇔ \beta S(0)/\gamma >1\\
\beta S(0)-\gamma =0 ⇔ \beta S(0)/\gamma =1\\
\beta S(0)-\gamma <0 ⇔ \beta S(0)/\gamma <1
\end{align}
にそれぞれ対応します。
\(\beta=\)0.000004, \(\gamma=\)0.05として,①, ②,③を解くと,図3が得られます。
計算手法は,①,②,③を差分方程式に変換し,適当な初期値を入力すれば繰り返しの計算になりますので,表計算ソフトのMicrosoft Excel(R)でも処理することが可能です。
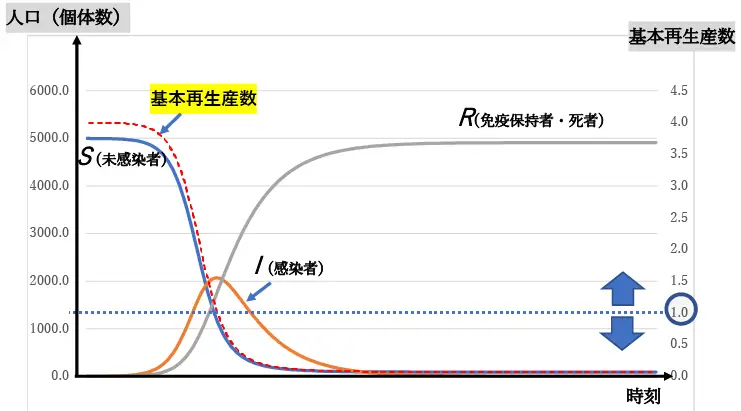 図3
図3
図3より, 以下のことがわかります。
・\(S\)(未感染者)は感染者に転じて時間とともに減少する傾向にあります。
・\(I\)(感染者)はやや遅れて増加し,ピークに達した後減少に転じます。
・\(R\)(免疫保持者・死者)は\(I\)に遅れて増加して,一定数に収束していきます。
基本再生産数は破線で示し,右の縦軸で基本再生産数を表します。図3からも
基本再生産数>1の期間では,\(I\)(感染者)は増加し,
基本再生産数<1の期間では,\(I\)(感染者)は減少する
ことが確認できます。
また,感染率\(\beta\)の値のみを増加させてみますと,\(I\)(感染者)は前倒し的に急速に増大してピークに達したあと,急激に減少する傾向になることがわかります。ここでは,Python(R)による計算結果を図4に示します。
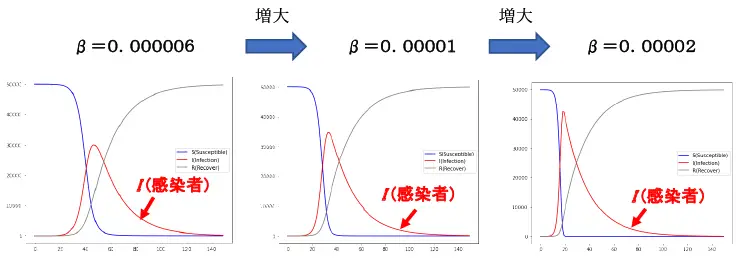 図4
図4
SIRモデルの拡張としてさまざまな数理モデルが研究・改良されていますが,ここでは2例ほどの数理モデルの概要のみを紹介します。また,これらのモデルの解析結果や優位性などについても,今後続編として紹介できればと考えています。
感染者\(I(t) \)を潜伏期(まだ感染性をもたない状態)の感染者\(E(t)\)と感染性をもつ状態の感染者\(I(t)\) に分けたもので,計4つの人口区分によりモデルを構成し,SEIRモデルとも呼びます。すなわち,SIRモデルでは3つの人口区分でしたが,より細かく4つの人口区分に分類しています。これは未感染者\(S(t)\)が感染者\(I(t)\)により感染したあと,即\(I(t)\)に転じるのではなく,いったん感染性をもたない潜伏期の人口区分\(E(t)\)を経るというタイムラグをもたせるモデルです。
以下に4個の微分方程式からなるSEIRモデルを示します。
\begin{cases}
\displaystyle\frac{dS(t)} {dt} =-\beta S(t)I(t) …⑤ \\
\displaystyle\frac{dE (t)} {dt} =\beta S(t)I(t)-\epsilon E(t) …⑥ \\
\displaystyle\frac{dI(t)} {dt} =\epsilon E(t)-\gamma I(t) …⑦\\
\displaystyle\frac{dR(t)} {dt} =\gamma I(t) …⑧
\end{cases}
\(\epsilon\):潜伏期後に感染性をもつ率
微分方程式⑤,⑥,⑦,⑧を図式化すると図5のようになります。
人口区分\(S\)と\(I\)の間に\(E\)(感染性をもたない潜伏期)の人口区分を設定していることに注目してください。
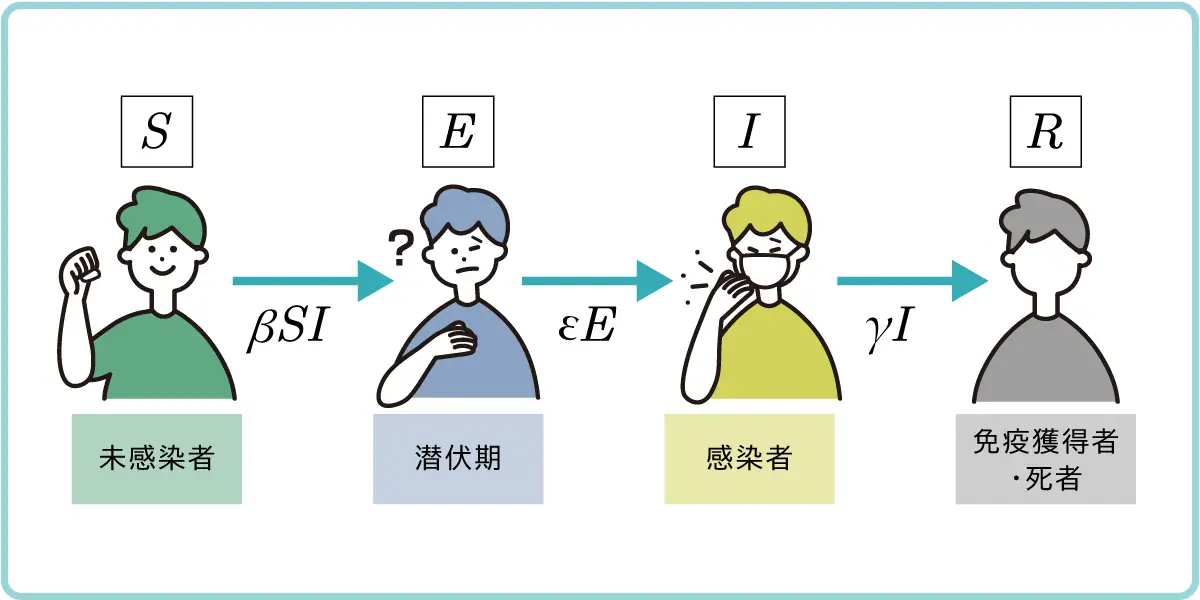 図5
図5
SIRモデルでは,3つの人口区分\(S(t)\),\(I(t)\),\(R(t)\) は時刻\(t\)のみの関数でしたが,ここでは,さらにそれぞれ年齢\(a\)の変数を加え,2変数\(a\),\(t\) の年齢密度関数\(s(a,t)\),\(i(a,t)\),\(r(a,t)\)を考えます。
たとえば,図6のように年齢密度関数\(p(a,t)\)であれば,時刻\(t\)における年齢階級[\(a_{1},a_{2} \)]である人口数\(P_{a_1∼a_2} (t) \)は
\(P_{a_1∼a_2} (t) =\int_{a_1}^{a_2}p(a,t)da\)
と積分で求めることができます。
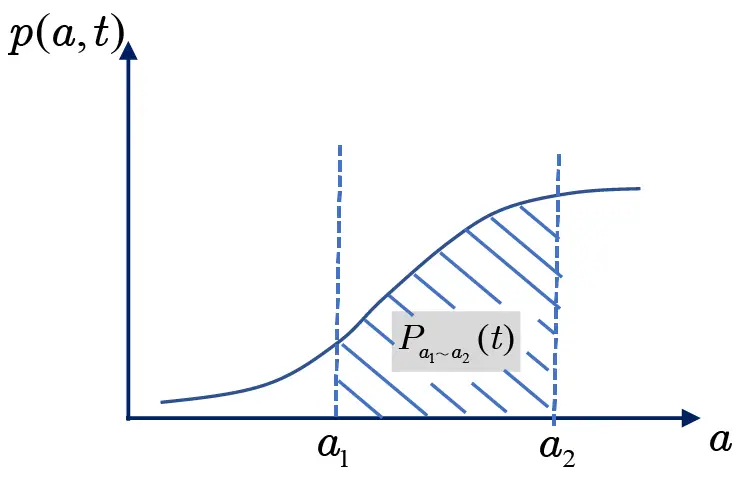 図6
図6
そこでSIRモデルにおける\(S(t)\),\(I(t)\),\(R(t)\)を\(S(t)\) → \(s(a,t)\),\(I(t)\) → \(i(a,t)\),\(R(t)\) → \(r(a,t)\)と置き換えて,それぞれ時刻\(t\)における未感染者,感染者,免疫獲得者(死者含む)の年齢密度関数とします。
また,\(p(a,t)=s(a,t)+i(a,t)+r(a,t) \)を全人口の年齢密度 \(\gamma(a)\),\(\delta(a)\),\(\lambda(a)\)をそれぞれ時刻\(t\)での年齢別の除去率,快復率,感染率 \(\mu(a)\)を年齢別死亡率(年齢別の感染以外で死亡する割合)とすれば,以下3個の連立偏微分方程式モデルが得られます。なお,このモデルでは免疫を獲得しないで快復する率\(\delta\)を考慮しております。
| \begin{cases} \displaystyle\frac{∂s(a,t)} {∂t}+\frac{∂s(a,t)} {∂a} =-\mu(a)s(a,t)-\lambda(a,t)s(a,t)+\delta(a)i(a,t) …⑨ \\ \displaystyle\frac{∂i(a,t)} {∂t}+\frac{∂i(a,t)} {∂a} =-\mu(a)i(a,t)+\lambda(a,t)s(a,t)-(\gamma(a)+\delta(a))i(a,t) …⑩ \\ \displaystyle\frac{∂r(a,t)} {∂t}+\frac{∂r(a,t)} {∂a} =-\mu(a)r(a,t)+γ(a)i(a,t) …⑪ \end{cases} |
ここで,
出生率:\(s(0,t)=b_1 (t)\),\(i(0,t)=b_2 (t)\),\(r(0,t)=b_3 (t)\)
初期条件:\(s(a,0)=s_0 (a)\),\(i(a,0)=i_0 (a)\),\(r(a,0)=r_0 (a)\)
上式⑨は,未感染者の年齢密度は未感染者自身の死亡と感染によって減少し,感染者の快復によって増加することを表します。
また⑩は,感染者の年齢密度は感染者自身の死亡によって減少し,未感染者の感染によって増加し,感染者自身の除去と快復によって減少することを表します。
最後に⑪は,免疫獲得者(死者含む)の年齢密度は,免疫獲得者(死者含む)自身の死亡によって減少し,感染者の除去によって増加することを表します。
上式⑨,⑩,⑪の数学的導出は省略します。くわしくは引用文献3を参照してください。
本記事では,おもに感染症拡大の古典的数理モデルであるSIRモデルの構造や基本的特徴を紹介しました。昨今の新型コロナウイルス感染症(COVID-19)への適用も動機となって,SIRモデルの拡張版,また独自の新しい数理的手法も次々と開発されています。しかし,数理モデルのみを用いて感染症の根本を解決できるものではなく,その適用限界をわきまえながら利用していく医療的アプローチと科学的知見を涵養していくことがきわめて重要と考えられます。
※MicrosoftおよびExcelは,米国 Microsoft Corporation の,米国およびその他の国における登録商標または商標です。
※Pythonは,Python Software Foundationの商標または登録商標です。

学習数学研究所 研究員